某商场计划拨款9万元从厂家购进50台电视机．已知该厂家生产三种不同型号的电视机，出厂价分别为：甲种每台1500元，乙种每台2100元，丙种每台2500元．
（1）若商场同时购进其中两种不同型号电视机共50台，用去9万元，请研究一下商场的进货方案；
（2）若商场销售一台甲种电视机可获利150元，销售一台乙种电视机可获利200元，销售一台丙种电视机可获利250元．在同时购进两种不同型号电视机的方案中，为使销售时获利最多，你选择哪种进货方案；
（3）若商场准备用9万元同时购进三种不同的电视机50台，请你设计进货方案．
解：（1）设购进甲种x台，乙种y台．
则有：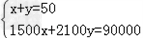
，
解得
；
设购进乙种x台，丙种y台．
则有：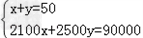
，
解得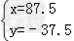
；（不合题意，舍去此方案）
设购进甲种x台，丙种y台．
则有：
，
解得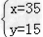
．
通过列方程组解得有以下两种方案成立：
①甲、乙两种型号的电视机各购25台．
②甲种型号的电视机购35台，丙种型号的电视机购15台；
（2）方案①获利为：25×150+25×200=8750；
方案②获利为：35×150+15×250=9000（元）．
所以为使销售时获利最多，应选择第②种进货方案；
（3）设购进甲种电视x台，乙种电视y台，则购进丙种电视的数量为：z=（50﹣x﹣y）台．
1500x+2100y+2500（50﹣x﹣y）=90000，
化简整理，得5x+2y=175．
又因为0＜x、y、z＜50，且均为整数，
所以上述二元一次方程只有四组解：
x=27，y=20，z=3；
x=29，y=15，z=6；
x=31，y=10，z=9；
x=33，y=5，z=12．
因此，有四种进货方案：
1、购进甲种电视27台，乙种电视20台，丙种电视3台，
2、购进甲种电视29台，乙种电视15台，丙种电视6台，
3、购进甲种电视31台，乙种电视10台，丙种电视9台，
4、购进甲种电视33台，乙种电视5台，丙种电视12台．